using System;
namespace ConsoleApp34
{
class Program
{
static void Main(string[] args)
{
const int N = 8;
//初始化时域数据
Complex[] TD2FD = new Complex[N];
for (int i = 0; i < N; i++)
{
Complex cpx = new Complex();
cpx.re = i;
cpx.im = 0;
TD2FD[i] = cpx;
}
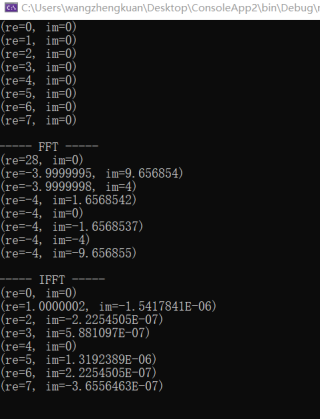
Console.WriteLine("------原始信号-----");
Print(TD2FD);
Console.WriteLine("----- FFT -----");
FFT(TD2FD);
Print(TD2FD);
Console.WriteLine("----- IFFT -----");
IFFT(TD2FD);
Print(TD2FD);
Console.Read();
}
//快速傅里叶变换
public static void FFT(Complex[] TD2FD)
{
FFT_Core(TD2FD, WT_LUT(TD2FD.Length, 1));
}
//快速傅里叶逆变换
public static void IFFT(Complex[] FD2TD)
{
//做FFT变换
Complex[] WT = WT_LUT(FD2TD.Length, -1);
FFT_Core(FD2TD, WT);
//实部除以N
for (int i = 0; i < FD2TD.Length; i++)
FD2TD[i].re /= FD2TD.Length;
}
// 返回旋转因子查询表(twiddle factor lookup table)
private static Complex[] WT_LUT(int N, int flag = 1)
{
Complex[] WT = new Complex[N];
for (int i = 0; i < N; i++)
{
Complex cpx_wt = new Complex();
float angle = (float)(-i * Math.PI * 2 / N);
cpx_wt.re = (float)Math.Cos(angle);
//IFFT flag=-1, FFT flag=1
cpx_wt.im = flag * (float)Math.Sin(angle);
WT[i] = cpx_wt;
}
return WT;
}
private static void FFT_Core(Complex[] TD2FD, Complex[] WT)
{
int power = (int)Math.Log(TD2FD.Length, 2);
int butterfly;
int p, s;
Complex x1, x2, wt;
BitReverse(TD2FD);
//蝶形运算
for (int k = 0; k < power; k++) //级数
{
//Console.WriteLine("第{0}级, 共{1}组", k, 1 << k);
for (int j = 0; j < 1 << k; j++) //组数
{
butterfly = 1 << (power - k);//每组有几个元素
//计算参与蝶形运算的两个元素的索引
p = j * butterfly;
s = p + butterfly / 2;
//Console.WriteLine("butterfly={0}, p={1}, s={2}", butterfly, p, s);
for (int i = 0; i < butterfly / 2; i++) //蝶形运算次数
{
//Console.Write(" ({0}x{1} wtIdx={2})", i + p, i + s, i * (1 << k));
x1 = TD2FD[i + p];
x2 = TD2FD[i + s];
wt = WT[i * (1 << k)];
TD2FD[i + p] = x1 + x2 * wt;
TD2FD[i + s] = x1 - x2 * wt;
}
//Console.WriteLine();
}
}
}
private static int BitReverse(int x)
{
//倒位排序
//0 1 2 3 4 5 6 7 十进制
//000 001 010 011 100 101 110 111 十进制对应的二进制
//000 100 010 110 001 101 011 111 码位反转
//0 4 2 6 1 5 3 7 码位反转后对应的十进制
int[] table = new int[8] { 0, 4, 2, 6, 1, 5, 3, 7 };
return table[x];
}
// 倒位排序——雷德算法
private static void BitReverse(Complex[] array)
{
int i, j, k;
int N = array.Length;
Complex temp;
j = 0;
for (i = 0; i < N - 1; i++)
{
if (i < j)
{
temp = array[i];
array[i] = array[j];
array[j] = temp;
}
// 求j的下一个倒序位
// N/2的二进制最高位为1,其他位都为0
// 判断最高位是否为1,可与N/2进行比较
// 判断次高位是否为1,可与N/4进行比较
k = N >> 1;
//如果k<=j,表示j的最高位为1
while (k <= j)
{
//当k<=j时,需要将最高位变为0
j = j - k;
//判断次高位是否为1,依次类推,逐个比较,直到j某个位为0
k >>= 1;
}
j = j + k;//将0变为1
}
}
// 打印
private static void Print(Complex[] TD2FD)
{
for (int i = 0; i < TD2FD.Length; i++)
{
Console.WriteLine("(re={0}, im={1})", TD2FD[i].re, TD2FD[i].im);
}
Console.WriteLine();
}
}
//定义复数
public class Complex
{
public float re;//实数部
public float im;//虚数部
public static Complex operator +(Complex lhs, Complex rhs)
{
Complex result = new Complex();
result.re = lhs.re + rhs.re;
result.im = lhs.im + rhs.im;
return result;
}
public static Complex operator -(Complex lhs, Complex rhs)
{
Complex result = new Complex();
result.re = lhs.re - rhs.re;
result.im = lhs.im - rhs.im;
return result;
}
public static Complex operator *(Complex lhs, Complex rhs)
{
Complex result = new Complex();
result.re = lhs.re * rhs.re;
result.im = lhs.im * rhs.im;
return result;
}
public static Complex operator *(float lhs, Complex rhs)
{
Complex result = new Complex();
result.re = lhs * rhs.re;
result.im = lhs * rhs.im;
return result;
}
public static Complex operator *(Complex lhs, float rhs)
{
Complex result = new Complex();
result.re = lhs.re * rhs;
result.im = lhs.im * rhs;
return result;
}
}
}
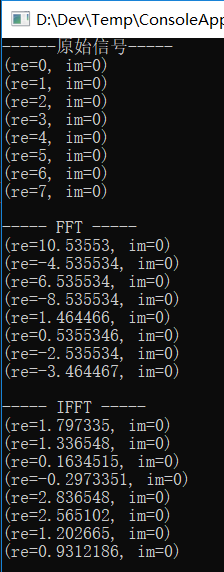
请问下我写的IFFT,为什么没还原成原始数据呢(re=0,1,2,3,4,5,6,7)?