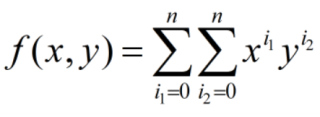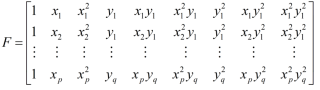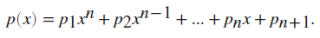MATLAB如何实现带等式和不等式约束条件的最小二乘法拟合多元多项式

Question

多元多项式的公式如图，现在有n个数据（x,y,f(x,y)）来拟合这个多项式，用最小二乘法，具体程序如下面的代码

Z=xlsread('Linton.xlsx');
x=Z(:,1);%x的数据，为风速，范围是0到40
y=Z(:,2);%y的数据，为风向，范围是0到360
z=Z(:,3);%频率数据
n = 7; % n为多项式的阶数，参数一共为(n+1)²个
p = length(x); q = length(y);
[X,Y,i1,i2] = ndgrid(x,y,0:n,0:n);
F = X.^i1.*Y.^i2;
F = reshape(F, p*q, (n+1)^2); %这一段是最小二乘法的左边矩阵，F矩阵具体形式如下图
A = F'*F;
b = F'*z;
a = A\b;%最小二乘法

然后现在就是得加入2个约束条件，一个是x在0到40，y在0到360，f(x,y)的积分等于1，然后f(x,y）永远大于0这两个约束条件。积分为1这个约束可以用拉格朗日乘子法来写。如果是下图的普通多项式，可以加下面一段代码解决积分为1

G = 1./(n+1:-1:1).*40.^(n+1:-1:1);% 这段是上图的普通多项式积分为1，直接写出了积分形式然后用拉格朗日乘子法
%现在需要对最上面的多元多项式积分为1，需要改成x在0到40，y在0到360的二重积分为1
aa = [A, F'; F, 0]\[b;1];%拉格朗日乘子法

现在是得把G矩阵写成二重积分，想问下这种多元多项式进行二重积分的代码应该怎么写。再就是f(x,y)永远大于0的约束要如何加上，以前只写过一维数据，然后普通多项式MATLAB也有代码，这个多元多项式得自己编写

Answer 1

你好，xy构成的多项式也可以写，但是比较繁琐，而且求解很难满足最后一个条件，全局大于0，下面是我的一维拓展方案：
主函数：

%% 为了得到分布，假设了一个协方差矩阵
mu=[20,180];%数学期望
sigma=[20/3 0;0,60].^2;%协方差矩阵
r=mvnrnd(mu,sigma,100000);%生成100000个样本
x = r(:,1);
y = r(:,2);
[X, Y, C, xmid, ymid] = ef2(x,y,21,21,[0,40],[0,360]);% ,50,50,[-3, 3],[-3, 3]
C = C/(18*2);
figure(1);clf;
bar3(C)
title('原先数据')
xtick = 1:size(C,2); xticklabel = xmid; % xtick和xticklabel一定要对应，长度相等
ytick = 1:size(C,1); yticklabel = ymid; % ytick和yticklabel一定要对应，长度相等
set(gca, 'xtick', xtick, 'xticklabel',xticklabel,...
    'ytick', ytick, 'yticklabel',yticklabel)
xlabel('X')
ylabel('Y')
x = X(:);
y = Y(:);
z = C(:);


n = 7; % n为多项式的阶数，参数一共为(n+1)²个
[i1, i2] = meshgrid(0:n);
F = arrayfun(@(i)x.^i1(i).*y.^i2(i), 1:numel(i1), 'uniform', 0);
F = cell2mat(F);

A = F'*F;
b = F'*z;
a = A\b;%最小二乘法

zfit1 = polyfunval(X,Y,a,n);
figure(2);clf;
bar3(zfit1)
xtick = 1:size(C,2); xticklabel = xmid; % xtick和xticklabel一定要对应，长度相等
ytick = 1:size(C,1); yticklabel = ymid; % ytick和yticklabel一定要对应，长度相等
set(gca, 'xtick', xtick, 'xticklabel',xticklabel,...
    'ytick', ytick, 'yticklabel',yticklabel)
title('最小二乘法')

G = arrayfun(@(i)40^(i1(i)+1)*360^(i2(i)+1)/((i1(i)+1)*(i2(i)+1)), 1:numel(i1));
aa = [A, G'; G,1]\[b;1];
zfit2 = polyfunval(X,Y,aa,n);
figure(3);clf;
bar3(zfit2)
fprintf('zfit最小值%f\n', min(zfit2(:)))
xtick = 1:size(C,2); xticklabel = xmid; % xtick和xticklabel一定要对应，长度相等
ytick = 1:size(C,1); yticklabel = ymid; % ytick和yticklabel一定要对应，长度相等
set(gca, 'xtick', xtick, 'xticklabel',xticklabel,...
    'ytick', ytick, 'yticklabel',yticklabel)
title('最小二乘法+拉格朗日乘子法（保证积分为1）')
pause(0.01)

a = getIniA(x,y,z,n);
options = optimoptions('fmincon','Algorithm','interior-point');% 
flag = -1; %设初始不收敛
f = @(a)myfun(a,x,y,z,n);
nlinf = @(a)nlinfunc(a,x,y,n);

while(flag<=0)
    ratio = 0.1;%如果长时间不收敛，减少n或者改动ratio再计算
    [aa,~,flag] = fmincon(f,a+ratio*(rand(size(a))-0.5).*a,[],[],G,1, [], [], nlinf,options);
end

多项式求值函数polyfunval.m

function f = polyfunval(x,y,a,n)
[i1, i2] = meshgrid(0:n);
Cfit = arrayfun(@(i)a(i)*x.^i1(i).*y.^i2(i), 1:numel(i1), 'uniform', 0);
f = Cfit{1};
for i = 2:numel(Cfit)
    f = f + Cfit{i};
end
end

目标函数：优化函数

function f = myfun(a,x,y,z,n)
zf = polyfunval(x,y,a,n);
f = norm(zf-z);
end

非线性约束

function [c,ceq] = nlinfunc(a,x,y,n)
F = polyfunval(x,y,a,n);
c = - min(F);
ceq = [];
end

分布统计函数

function [X, Y, CDF, xmid, ymid] = ef2(x,y,nx,ny,xminmax,yminmax)
% x：x的值
% y：y的值
% nx：x方向划分段数
% ny：y方向划分段数
% xminmax = [xmin, xmax]
% yminmax = [ymin, ymax]
num = length(x);
if(num~=length(y))
   error('输入的x和y长度必须相等') 
end
if(nargin>6) % 如果变量个数大于6个，太多了
    error('太多输入变量')
elseif(nargin<2) % 如果变量个数小于2个，太少了
    error('输入变量数目不足!!')
end
if(nargin==6) % 如果变量个数等于6个，赋值给ymin和ymax
    ymin = yminmax(1);
    ymax = yminmax(2);
end
if(nargin>=5)% 如果变量个数大于等于5个，赋值给xmin和xmax
    xmin = xminmax(1);
    xmax = xminmax(2);
end
if(nargin<=4)% 如果变量个数小于等于4个，自定义xmin和xmax
    xmin = min(x);
    xmax = max(x)+eps;
    ymin = min(y);
    ymax = max(y)+eps;
end
if(nargin<=3)% 如果变量个数小于等于3个，自定义y方向划分段数ny
    ny = 30;
end
if(nargin==2)% 如果变量个数等于2个，自定义x方向划分段数nx
    nx = 30;
end
xg = linspace(xmin, xmax, nx);%x方向的点
yg = linspace(ymin, ymax, ny);%y方向的点
xmid = (xg(1:end-1)+xg(2:end))/2;
ymid = (yg(1:end-1)+yg(2:end))/2;
[X,Y] = meshgrid(xmid, ymid);%形成网格
[I,J] = meshgrid(2:nx, 2:ny);%下标网格
CDF = arrayfun(@(i,j)sum(x>=xg(i-1)&x<xg(i)&y<yg(j)&y>=yg(j-1))/num,I,J);%形成经验分布
end

初始化参数函数

function aa = getIniA(x,y,z, n)
 % n为多项式的阶数，参数一共为(n+1)²个
[i1, i2] = meshgrid(0:n);
F = arrayfun(@(i)x.^i1(i).*y.^i2(i), 1:numel(i1), 'uniform', 0);
F = cell2mat(F);
A = F'*F;
b = F'*z;
G = arrayfun(@(i)40^(i1(i)+1)*360^(i2(i)+1)/((i1(i)+1)*(i2(i)+1)), 1:numel(i1));
aa = [A, G'; G,1]\[b;1];
aa = aa(1:end-1);
end

最后可见zfit最小值为-1e-7，很小（但不是正数），只满足了多项式拟合和积分为1的优化。全局为0搜索非常久也难得到结果，可能原因在于系数太过于敏感，因为360的7次方非常大，而1的7次方又特别小。