MATLAB 解线性方程组

Question

按题目要求用顺序消元法，列主元消元法和追赶法求方程组的解，想求个思路和全过程代码。不知道为什么我写的代码MATLAB上算不出结果，想看看正确的代码。

Answer 1

基于Monster 组和GPT的调写：
2

% 定义系数矩阵和常数向量
A = [0.001 2.000 3.000; -1.000 3.712 4.623; -2.000 1.072 5.643];
b = [1.000; 2.000; 3.000];

% 顺序消元法求解
x1 = A\b;

% 列主元消元法求解
[L,U,P] = lu(A);
y = L\(P*b);
x2 = U\y;

% 输出结果并与真实解进行比较
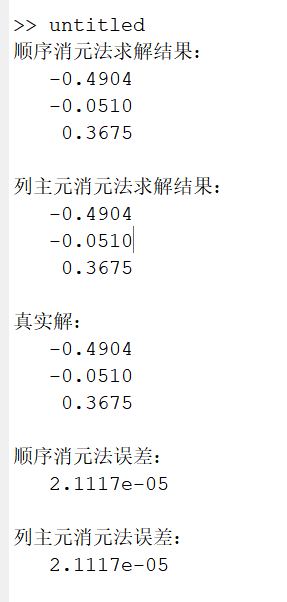
fprintf('顺序消元法求解结果：\n');
disp(x1);
fprintf('列主元消元法求解结果：\n');
disp(x2);
fprintf('真实解：\n');
x_true = [-0.4904; -0.05104; 0.3675];
disp(x_true);

fprintf('顺序消元法误差：\n');
disp(norm(x1 - x_true));
fprintf('列主元消元法误差：\n');
disp(norm(x2 - x_true));

4

% 定义系数矩阵
A = [2 -1 0 0; -1 2 -1 0; 0 -1 2 -1; 0 0 -1 2];
% 定义右侧常数向量
b = [0; 0; 0; 5];

% 使用追赶法求解线性方程组
n = length(b);
c = diag(A, -1);
d = diag(A);
e = diag(A, 1);
% 前向消元
for i = 2:n
    factor = c(i-1) / d(i-1);
    d(i) = d(i) - factor * e(i-1);
    b(i) = b(i) - factor * b(i-1);
end
% 回代求解
x = zeros(n, 1);
x(n) = b(n) / d(n);
for i = n-1:-1:1
    x(i) = (b(i) - e(i) * x(i+1)) / d(i);
end

% 输出解向量
disp(x);

4.顺序消元法

% 定义系数矩阵和常数向量
A = [1.1348, 3.8326, 1.1651, 3.4017;
     0.5301, 1.7875, 2.5330, 1.5435;
     3.4129, 4.9317, 8.7643, 1.3142;
     1.2371, 4.9998, 10.6721, 0.0147];
b = [9.5342; 6.3941; 18.4231; 16.9237];

% 高斯消元求解方程组
n = length(b);
for k = 1:n-1
    for i = k+1:n
        factor = A(i,k)/A(k,k);
        A(i,k+1:n) = A(i,k+1:n) - factor*A(k,k+1:n);
        b(i) = b(i) - factor*b(k);
    end
end

% 回代求解方程组
x = zeros(n,1);
x(n) = b(n)/A(n,n);
for i = n-1:-1:1
    x(i) = (b(i) - A(i,i+1:n)*x(i+1:n))/A(i,i);
end

% 输出结果
disp('顺序消元法结果：');
disp(x);

列主元消元法

% 定义系数矩阵和常数向量
A = [1.1348, 3.8326, 1.1651, 3.4017;
     0.5301, 1.7875, 2.5330, 1.5435;
     3.4129, 4.9317, 8.7643, 1.3142;
     1.2371, 4.9998, 10.6721, 0.0147];
b = [9.5342; 6.3941; 18.4231; 16.9237];

% 列主元消元求解方程组
n = length(b);
for k = 1:n-1
    [~,maxidx] = max(abs(A(k:n,k)));  % 找到当前列中绝对值最大的元素所在行
    maxidx = maxidx + k - 1;
    if A(maxidx,k) == 0   % 避免主元为0的情况
        error('矩阵不可逆');
    end
    % 交换当前行和主元所在行
    if maxidx ~= k
        A([k,maxidx],k:n) = A([maxidx,k],k:n);
        b([k,maxidx]) = b([maxidx,k]);
    end
    % 消元
    for i = k+1:n
        factor = A(i,k)/A(k,k);
        A(i,k+1:n) = A(i,k+1:n) - factor*A(k,k+1:n);
        b(i) = b(i) - factor*b(k);
    end
end

% 回代求解方程组
x = zeros(n,1);
x(n) = b(n)/A(n,n);
for i = n-1:-1:1
    x(i) = (b(i) - A(i,i+1:n)*x(i+1:n))/A(i,i);
end

% 输出结果
disp('列主元消元法结果：');
disp(x);