决策树的相关问题，ID3算法

Question

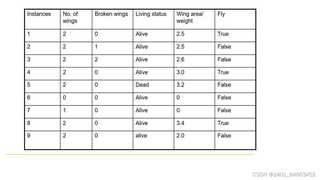
问题作用ID3算法，建立决策树第一个节点，写出信息增益求解过程。

Answer 1

引自免费微信小程序：皆我百晓生

为了解答这个问题，我们首先需要理解ID3算法的基本原理，然后根据给定的数据集计算信息增益，并确定决策树的第一个节点。ID3算法基于信息论中的熵和信息增益概念，选择具有最大信息增益的属性作为当前节点的分裂属性。

步骤一：计算数据集的熵

首先，我们计算整个数据集D的熵，记作Entropy(D)。熵是衡量不确定性的一种度量。对于分类问题，熵定义为：

[ Entropy(D) = -\sum_{i=1}^{c} p_i \log_2(p_i) ]

其中，(p_i)是第i类样本在数据集中所占的比例，c是类别总数。

在这个例子中，我们有两个类别：“Alive”和“Dead”，分别有7个和2个实例。

[ Entropy(D) = -\left( \frac{7}{9} \log_2\left(\frac{7}{9}\right) + \frac{2}{9} \log_2\left(\frac{2}{9}\right) \right) ]

步骤二：计算每个属性的信息增益

我们需要对每个可能的属性（"Broken wings", "Living status", "Wing area", "Fly wings weight"）计算信息增益。信息增益定义为：

[ Gain(D, A) = Entropy(D) - \sum_{v \in values(A)} \frac{|D_v|}{|D|} Entropy(D_v) ]

其中，A是属性，values(A)是A的所有可能值，(D_v)是属性A取值为v的子集。

计算"Broken wings"的信息增益

1. 当"Broken wings"的值为0时，有2个实例（实例5和6），全部是“Dead”。因此，Entropy(0) = 0。
2. 当"Broken wings"的值为1时，有2个实例（实例2和7），1个“Alive”，1个“Dead”。Entropy(1) = 1。
3. 当"Broken wings"的值为2时，有5个实例（实例1, 3, 4, 8, 9），4个“Alive”，1个“Dead”。Entropy(2) = ( -\left( \frac{4}{5} \log_2\left(\frac{4}{5}\right) + \frac{1}{5} \log_2\left(\frac{1}{5}\right) \right) )

[ Gain(D, "Broken wings") = Entropy(D) - \left( \frac{2}{9} \cdot 0 + \frac{2}{9} \cdot 1 + \frac{5}{9} \cdot Entropy(2) \right) ]

计算其他属性的信息增益

同样的方式，我们可以计算出其他属性的信息增益。

步骤三：选择具有最大信息增益的属性

比较所有属性的信息增益，选择最大的一个作为决策树的根节点。

代码示例

import math

# 数据集
data = [
    {"Broken wings": 2, "Living status": "Alive", "Wing area": 2.5, "Fly wings weight": True},
    {"Broken wings": 2, "Living status": "Alive", "Wing area": 2.5, "Fly wings weight": False},
    {"Broken wings": 2, "Living status": "Alive", "Wing area": 2.6, "Fly wings weight": False},
    {"Broken wings": 2, "Living status": "Alive", "Wing area": 3.0, "Fly wings weight": True},
    {"Broken wings": 2, "Living status": "Dead", "Wing area": 3.2, "Fly wings weight": False},
    {"Broken wings": 0, "Living status": "Alive", "Wing area": 0, "Fly wings weight": False},
    {"Broken wings": 1, "Living status": "Alive", "Wing area": 0, "Fly wings weight": False},
    {"Broken wings": 2, "Living status": "Alive", "Wing area": 3.4, "Fly wings weight": True},
    {"Broken wings": 2, "Living status": "Alive", "Wing area": 2.0, "Fly wings weight": False}
]

# 计算熵
def entropy(data):
    alive = dead = 0
    for d in data:
        if d["Living status"] == "Alive":
            alive += 1
        else:
            dead += 1
    total = alive + dead
    if alive == 0 or dead == 0:
        return 0
    return -(alive/total * math.log2(alive/total) + dead/total * math.log2(dead/total))

# 计算信息增益
def gain(data, attr):
    attr_values = set([d[attr] for d in data])
    total_entropy = entropy(data)
    weighted_entropy = 0
    for value in attr_values:
        subset = [d for d in data if d[attr] == value]
        weighted_entropy += len(subset)/len(data) * entropy(subset)
    return total_entropy - weighted_entropy

# 计算各属性的信息增益
gains = {attr: gain(data, attr) for attr in data[0].keys() if attr != "Living status"}

# 找到最大信息增益的属性
best_attr = max(gains, key=gains.get)
print("Best attribute:", best_attr)

这个代码片段将计算并输出具有最大信息增益的属性，即决策树的第一个节点。请注意，实际运行此代码前，应确保环境已安装Python解释器。