请教下关于FFT算法生成频谱图的问题

Question

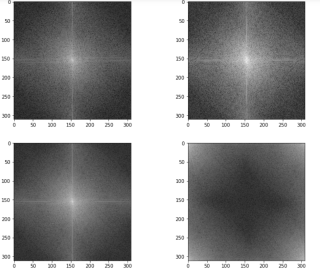
我理解的大体思路是：

1、将图像的灰度值作为输入数据代入FFT算法，生成结果A

2、直接用A的实部值作为像素值生成频谱图

但是我发现生成的频谱图布局不对。

用幅度值作为像素值生成的频谱图

现在我有3个疑问：

1、将图像灰度值数据代入FFT，再直接IFFT，得到一张正确的灰度图像，是否说明写的FFT和IFFT算法没问题？

2、频谱图的像素值是由FFT结果数据的实部值生成吗？

3、代码中的中心化方法FFT2Shift()是我这样写的吗（不确定对公式是否理解正确）？

 

在线对图像做傅里叶变换 https://sci2fig.herokuapp.com/fourier

 

下面给出我封装的傅里叶变换类

using System;

/// <summary>
/// 傅里叶变换
/// </summary>
public sealed class Fourier
{
    //快速傅里叶变换
    public static void FFT(Complex[] TD2FD)
    {
        FFT_Core(TD2FD, WT_LUT(TD2FD.Length, 1));
    }

    //快速傅里叶变换 (二维)
    public static void FFT2(Complex2D TD2FD)
    {
        //对每一行做FFT
        for (int i = 0; i < TD2FD.Height; i++)
        {
            Complex[] row = TD2FD.GetRow(i);
            FFT(row);
            TD2FD.SetRow(i, row);
        }

        //对每一列做FFT
        for (int i = 0; i < TD2FD.Width; i++)
        {
            Complex[] column = TD2FD.GetColumn(i);
            FFT(column);
            TD2FD.SetColumn(i, column);
        }
    }

    //快速傅里叶逆变换
    public static void IFFT(Complex[] FD2TD)
    {
        //做FFT变换
        Complex[] WT = WT_LUT(FD2TD.Length, -1);
        FFT_Core(FD2TD, WT);
        //实部除以N
        for (int i = 0; i < FD2TD.Length; i++)
            FD2TD[i].re /= FD2TD.Length;
    }

    //快速傅里叶逆变换 (二维)
    public static void IFFT2(Complex2D FD2TD)
    {
        //对每一行做IFFT
        for (int i = 0; i < FD2TD.Height; i++)
        {
            Complex[] row = FD2TD.GetRow(i);
            IFFT(row);
            FD2TD.SetRow(i, row);
        }

        //对每一列做IFFT
        for (int i = 0; i < FD2TD.Width; i++)
        {
            Complex[] column = FD2TD.GetColumn(i);
            IFFT(column);
            FD2TD.SetColumn(i, column);
        }
    }

    // 将直流分量移到频谱图的中心
    public static void FFT2Shift(Complex2D complex2D)
    {
        int halfH = complex2D.Height / 2;
        int halfW = complex2D.Width / 2;
        //将图像四个象限区域按对角线交换
        for (int i=0; i<halfH; i++)
        {
            for (int j=0; j<complex2D.Width; j++)
            {
                if (j < halfW)
                    complex2D.SwapComplex(i, j, i + halfH, j + halfW);
                else
                    complex2D.SwapComplex(i, j, i + halfH, j - halfW);
            }
        }
    }

    // 高通滤波
    public static void HighPassFilting(Complex2D complex2D)
    {
        int halfH = complex2D.Height / 2;
        int halfW = complex2D.Width / 2;
        int H4 = complex2D.Height / 8;
        int W4 = complex2D.Width / 8;
        for (int i = halfH - H4; i < halfH + H4; i++)
        {
            for (int j = halfW - W4; j < halfW + W4; j++)
            {
                Complex cpx = complex2D.GetComplex(i, j);
                cpx.re = 0;
                cpx.im = 0;
                complex2D.SetComplex(i, j, cpx);
            }
        }
    }

    // 低通滤波
    public static void LowPassFilting(Complex2D complex2D)
    {
        int halfH = complex2D.Height / 2;
        int halfW = complex2D.Width / 2;
        int H4 = complex2D.Height / 8;
        int W4 = complex2D.Width / 8;
        for (int i=0; i < complex2D.Height; i++)
        {
            for (int j=0; j < complex2D.Width; j++)
            {
                if (i < halfH - H4 || i > halfH + H4 ||
                    j < halfW - W4 || j > halfW + W4)
                {
                    Complex cpx = complex2D.GetComplex(i, j);
                    cpx.re = 0;
                    cpx.im = 0;
                    complex2D.SetComplex(i, j, cpx);
                }
            }    
        }
    }

    // 返回旋转因子查询表(twiddle factor lookup table)
    private static Complex[] WT_LUT(int N, int flag = 1)
    {
        Complex[] WT = new Complex[N];
        for (int i = 0; i < N; i++)
        {
            Complex cpx_wt = new Complex();
            float angle = (float)(-i * Math.PI * 2 / N);
            cpx_wt.re = (float)Math.Cos(angle);
            //IFFT flag=-1, FFT flag=1
            cpx_wt.im = flag * (float)Math.Sin(angle);
            WT[i] = cpx_wt;
        }
        return WT;
    }

    private static void FFT_Core(Complex[] TD2FD, Complex[] WT)
    {
        int power = (int)Math.Log(TD2FD.Length, 2);
        int butterfly;
        int p, s;
        Complex x1, x2, wt;

        //倒位排序
        BitReverse(TD2FD);

        //蝶形运算
        for (int k = 0; k < power; k++) //级数
        {
            for (int j = 0; j < 1 << (power - k - 1); j++) //组数
            {
                //每组有几个元素
                butterfly = 1 << k + 1;
                //计算参与蝶形运算的两个元素的索引
                p = j * butterfly;
                s = p + butterfly / 2;
                for (int i = 0; i < butterfly / 2; i++) //蝶形运算次数
                {
                    x1 = TD2FD[i + p];
                    x2 = TD2FD[i + s];
                    wt = WT[i * TD2FD.Length / butterfly];
                    TD2FD[i + p] = x1 + x2 * wt;
                    TD2FD[i + s] = x1 - x2 * wt;
                }
            }
        }
    }

    // 倒位排序——雷德算法
    private static void BitReverse(Complex[] array)
    {
        //倒位排序原理
        //0   1   2   3   4   5   6   7   十进制
        //000 001 010 011 100 101 110 111 十进制对应的二进制
        //000 100 010 110 001 101 011 111 码位反转
        //0   4   2   6   1   5   3   7   码位反转后对应的十进制

        int i, j, k;
        int N = array.Length;
        Complex temp;
        j = 0;

        for (i = 0; i < N - 1; i++)
        {
            if (i < j)
            {
                temp = array[i];
                array[i] = array[j];
                array[j] = temp;
            }
            // 求j的下一个倒序位
            // N/2的二进制最高位为1，其他位都为0
            // 判断最高位是否为1，可与N/2进行比较
            // 判断次高位是否为1，可与N/4进行比较
            k = N >> 1;
            //如果k<=j,表示j的最高位为1
            while (k <= j)
            {
                //当k<=j时，需要将最高位变为0
                j = j - k;
                //判断次高位是否为1,依次类推，逐个比较，直到j某个位为0
                k >>= 1;
            }
            j = j + k;//将0变为1
        }
    }

    // 打印
    public static void Print(Complex[] TD2FD)
    {
        for (int i = 0; i < TD2FD.Length; i++)
        {
            Console.WriteLine(TD2FD[i].ToString());
        }
        Console.WriteLine();
    }
}

//定义复数
public class Complex
{
    public float re;//实数部
    public float im;//虚数部

    // 幅值
    public double Amplitude
    {
        get
        {
            //测试发现取值范围为
            //min=0.0009918213, max=412.4615
            return Math.Sqrt(re * re + im * im);
        }
    }

    // 频谱图像素值
    public double PixelAmplitude
    {
        get
        {
            //幅值范围很大,需要做以下处理:
            //1. 将幅值范围调到 [1, ?]
            //2. 利用Log函数压缩范围
            //3. 将范围映射到颜色值[0,1]
            double p = Math.Log(Amplitude * 10000) / 16f;
            return p;
        }
    }

    // 相位
    public double Phase
    {
        get
        {
            return Math.Atan2(im, re);
        }
    }

    public override string ToString()
    {
        return string.Format("re={0}, im={1}", re, im);
    }

    public static Complex operator +(Complex lhs, Complex rhs)
    {
        Complex result = new Complex();
        result.re = lhs.re + rhs.re;
        result.im = lhs.im + rhs.im;
        return result;
    }

    public static Complex operator -(Complex lhs, Complex rhs)
    {
        Complex result = new Complex();
        result.re = lhs.re - rhs.re;
        result.im = lhs.im - rhs.im;
        return result;
    }

    public static Complex operator *(Complex lhs, Complex rhs)
    {
        Complex result = new Complex();
        result.re = lhs.re * rhs.re - lhs.im * rhs.im;
        result.im = lhs.re * rhs.im + lhs.im * rhs.re;
        return result;
    }

    public static Complex operator *(float lhs, Complex rhs)
    {
        Complex result = new Complex();
        result.re = lhs * rhs.re;
        result.im = lhs * rhs.im;
        return result;
    }

    public static Complex operator *(Complex lhs, float rhs)
    {
        Complex result = new Complex();
        result.re = lhs.re * rhs;
        result.im = lhs.im * rhs;
        return result;
    }
}

public class Complex2D
{
    private Complex[,] matrix;
    private int m_width;
    private int m_height;

    // width:图像宽度 height:图像高度
    public Complex2D(int width, int height)
    {
        m_width = width;
        m_height = height;
        matrix = new Complex[width, height];
    }

    public int Width { get { return m_width; } }
    public int Height { get { return m_height; } }

    public Complex[] GetRow(int i)
    {
        Complex[] row = new Complex[m_width];
        for (int j = 0; j < m_width; j++)
            row[j] = matrix[j,i];
        return row;
    }

    public void SetRow(int i, Complex[] array)
    {
        for (int j = 0; j < m_width; j++)
            matrix[j, i] = array[j];
    }

    public Complex[] GetColumn(int i)
    {
        Complex[] column = new Complex[m_height];
        for (int j = 0; j < m_height; j++)
            column[j] = matrix[i,j];
        return column;
    }

    public void SetColumn(int i, Complex[] array)
    {
        for (int j = 0; j < m_width; j++)
            matrix[i, j] = array[j];
    }

    //i: 第几行  j: 第几列
    public Complex GetComplex(int i, int j)
    {
        return matrix[j,i];
    }

    //i: 第几行  j: 第几列
    public void SetComplex(int i, int j, Complex src)
    {
        matrix[j, i] = src;
    }

    // 交换两个元素
    // i: 第几行  j: 第几列
    public void SwapComplex(int i0, int j0, int i1, int j1)
    {
        Complex tmp = matrix[j0,i0];
        matrix[j0, i0] = matrix[j1, i1];
        matrix[j1, i1] = tmp;
    }

    // 交换行
    public void SwapRow(int i, int j)
    {
        for (int k=0; k<m_width; k++)
        {
            Complex cpx0 = matrix[k,i];
            Complex cpx1 = matrix[k,j];
            matrix[k,i] = cpx1;
            matrix[k,j] = cpx0;
        }
    }

    // 交换列
    public void SwapColumn(int i, int j)
    {
        for (int k = 0; k < m_height; k++)
        {
            Complex cpx0 = matrix[i,k];
            Complex cpx1 = matrix[j,k];
            matrix[i,k] = cpx1;
            matrix[j,k] = cpx0;
        }
    }

    public void Print(string fileName)
    {
        System.Text.StringBuilder sb = new System.Text.StringBuilder();
        for (int i = 0; i < m_height; i++)
        {
            for (int j = 0; j < m_width; j++)
                sb.AppendFormat("{0:G} ", matrix[j,i].re.ToString().PadRight(5));
            sb.AppendLine();
        }
        System.IO.File.WriteAllText(string.Format("D://{0}.txt", fileName), sb.ToString());
    }
}

我的测试是在Unity中做的，下面给出我的辅助类

using UnityEngine;

public sealed class FourierHelper
{
    public static Texture2D ToTexture2D(Complex2D complex2D)
    {
        Texture2D tex = new Texture2D(complex2D.Width, complex2D.Height, TextureFormat.RGBA32, false);
        for (int i = 0; i < complex2D.Height; i++)
        {
            Complex[] cpxs = complex2D.GetRow(i);
            for (int j = 0; j < cpxs.Length; j++)
            {
                Complex cpx = cpxs[j];
                tex.SetPixel(j, i, new Color(cpx.re, cpx.re, cpx.re));
            }
        }
        tex.Apply();
        return tex;
    }

    // 转成频谱图
    public static Texture2D ToSpectrumTexture2D(Complex2D complex2D)
    {
        float min = float.MaxValue;
        float max = float.MinValue;
        Texture2D tex = new Texture2D(complex2D.Width, complex2D.Height, TextureFormat.RGBA32, false);
        for (int i = 0; i < complex2D.Height; i++)
        {
            Complex[] cpxs = complex2D.GetRow(i);
            for (int j = 0; j < cpxs.Length; j++)
            {
                Complex cpx = cpxs[j];
                float p = (float)cpx.PixelAmplitude;
                tex.SetPixel(j, i, new Color(p, p, p));
                if (p < min)
                    min = p;
                if (p > max)
                    max = p;
            }
        }
        tex.Apply();
        return tex;
    }

    public static Complex2D ToComplex2D(Texture2D tex)
    {
        Complex2D complex2D = new Complex2D(tex.width, tex.height);

        for (int y = 0; y < tex.height; y++)
        {
            for (int x = 0; x < tex.width; x++)
            {
                Color c = tex.GetPixel(x, y);
                Complex cpx = new Complex();
                cpx.re = c.r * 0.3f + c.g * 0.59f + c.b * 0.11f; //灰度值
                cpx.im = 0;
                complex2D.SetComplex(y, x, cpx);
            }
        }

        return complex2D;
    }
}

FFT->IFFT测试代码

using UnityEngine;
using UnityEngine.UI;
/// <summary>
/// 测试FFT->IFFT算法
/// </summary>
public class FFT_IFFT_Test : MonoBehaviour
{
    public RawImage rawImage;

    private void Start()
    {
        Texture2D tex = rawImage.texture as Texture2D;
        Complex2D complex2D = FourierHelper.ToComplex2D(tex);

        Fourier.FFT2(complex2D);
        Fourier.IFFT2(complex2D);

        Texture2D ifft_tex = FourierHelper.ToTexture2D(complex2D);
        rawImage.texture = ifft_tex;
    }
}

频谱图生成代码

using UnityEngine;
using UnityEngine.UI;
/// <summary>
/// 显示频谱图
/// </summary>
public class SpectrumTexture : MonoBehaviour
{
    public RawImage rawImage;

    private void Start()
    {
        Texture2D tex = rawImage.texture as Texture2D;
        Complex2D complex2D = FourierHelper.ToComplex2D(tex);

        Fourier.FFT2(complex2D);

        Texture2D sp_tex = FourierHelper.ToTexture2D(complex2D);
        rawImage.texture = sp_tex;
    }
}

如有需要也可下载我的测试工程(Unity)

链接：https://pan.baidu.com/s/1B62muufCP-tWQklPT5H49Q 
提取码：z6ku 

 

补充：IFFT2未还原数据

@ 皮皮宽

Answer 1

先说你程序的错误：

傅里叶变换和逆变换都没毛病，但你的二维复数矩阵的定义，错了；

我标出来了，你自己应该能改出来

public class Complex2D
{
    private List<Complex[]> rows = new List<Complex[]>();
    private List<Complex[]> columns = new List<Complex[]>();
    private int m_width;
    private int m_height;
 
    public Complex2D(int width, int height)
    {
        m_width = width;
        m_height = height;
        for (int i = 0; i < height; i++)
            rows.Add(new Complex[width]);   //row[0]~row[height-1]
        for (int i = 0; i < width; i++)
            columns.Add(new Complex[height]);//columns[0]~columns[height-1]
    }                                        //你这里相当于定义了两个矩阵，一个是行向量组成，一个列向量组成；按你的思路，你后面的应该始终保持这两个矩阵相等才对；
 
    public int Width { get { return m_width; } }
    public int Height { get { return m_height; } }
 
    public Complex[] GetRow(int i)
    {
        return rows[i];
    }
 
    public Complex[] GetColumn(int i)
    {
        return columns[i];
    }
 
    public void SetRow(int i, Complex[] src)
    {
        rows[i] = src;  //你只行向量？？你如果改了第一行的值，那每一列的第一个值也就跟着变了，你没改，你如果此时读第一列的值，你会发现row[i][j],columns[j][i],不一样
    }
 
    public void SetColumn(int i, Complex[] src)
    {
        columns[i] = src;  //和上面同理
    }
 
    //i: 第几行  j: 第几列
    public Complex GetComplex(int i, int j)
    {
        return rows[i][j];  //你的更改行和列有问题，columns[j][i]和row[i][j]不一样了
    }
 
    //i: 第几行  j: 第几列
    public void SetComplex(int i, int j, Complex src)
    {
        rows[i][j] = src;   //额。。。。你这里行和列改了，说明你注意到了，然而前面却不改。。
        columns[j][i] = src;
    }
 
    public void SetComplexs(Complex[][] src)
    {
        for (int i = 0; i < src.Length; i++)
        {
            Complex[] row = src[i];      //这里你又是只改变了row的值，不改columns
            for (int j = 0; j < row.Length; j++)
                SetComplex(i, j, row[j]);
        }
    }
 
    public void Print()
    {
        for (int i = 0; i < rows.Count; i++)
        {
            Complex[] row = rows[i];
            for (int j = 0; j < row.Length; j++)
                Console.Write("{0:G} ", row[j].re.ToString().PadRight(5));
            Console.WriteLine();
        }
        Console.WriteLine();
    }
}

 

1.你的傅里叶变换没问题；我看了几遍，确实找不出有啥问题；

2.是幅度（模），还要考虑复数部；

3.应该不对，我记得中心化应该是把矩阵分成四块，重新排序，你写的shift没看懂什么意思，不过就算不考虑中心化，你的图也不对；

下面四张图分别是，中心化后的实部，虚部，幅度，和未中心化的幅度谱

C#我不太懂，我用python写的，求幅度（模），然后中心化，在取对数：

freq = 20*np.log10(0.01 + np.abs(fp.fftshift(freq1)))；

看你的情况，应该把二维复数那一块改一改应该就好了