python PSO 粒子群算法 多元函数求极小值问题 运行结果和迭代次数每次都不一样

# -*- coding: utf-8 -*-
import math
import random
import numpy as np
import matplotlib.pyplot as plt
import pylab as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
class PSO:
def __init__(self, dimension, time, size, low, up, v_low, v_high, a, b):
# 初始化
self.dimension = dimension # 变量个数
self.time = time # 迭代的代数
self.size = size # 种群大小
self.bound = [] # 变量的约束范围
self.bound.append(low)
self.bound.append(up)
self.v_low = v_low
self.v_high = v_high
self.x = np.zeros((self.size, self.dimension)) # 所有粒子的位置
self.v = np.zeros((self.size, self.dimension)) # 所有粒子的速度
self.p_best = np.zeros((self.size, self.dimension)) # 每个粒子最优的位置
self.g_best = np.zeros((1, self.dimension))[0] # 全局最优的位置
self.a = a
self.b = b
# 初始化第0代初始全局最优解
temp = 1000000
for i in range(self.size):
for j in range(self.dimension):
self.x[i][j] = random.uniform(self.bound[0][j], self.bound[1][j])
self.v[i][j] = random.uniform(self.v_low, self.v_high)
self.p_best[i] = self.x[i] # 储存最优的个体
fit = self.fitness(self.p_best[i])
# 做出修改
if fit < temp:
self.g_best = self.p_best[i]
temp = fit
def fitness(self, x):
"""
个体适应值计算
"""
x1 = x[0]
x2 = x[1]
x3 = x[2]
x4 = x[3]
for i in range(11):
y = (a[i] - (x1 * (1 + b[i] * x2))/(1 + b[i] * x3 + x4 * b[i] * b[i]))**2
# print(y)
return y
def update(self, size):
c1 = 1.5 # 学习因子
c2 = 1.5
w = 0.8 # 自身权重因子
for i in range(size):
# 更新速度(核心公式)
self.v[i] = w * self.v[i] + c1 * random.uniform(0, 1) * (
self.p_best[i] - self.x[i]) + c2 * random.uniform(0, 1) * (self.g_best - self.x[i])
# 速度限制
for j in range(self.dimension):
if self.v[i][j] < self.v_low:
self.v[i][j] = self.v_low
if self.v[i][j] > self.v_high:
self.v[i][j] = self.v_high
# 更新位置
self.x[i] = self.x[i] + self.v[i]
# 位置限制
for j in range(self.dimension):
if self.x[i][j] < self.bound[0][j]:
self.x[i][j] = self.bound[0][j]
if self.x[i][j] > self.bound[1][j]:
self.x[i][j] = self.bound[1][j]
# 更新p_best和g_best
if self.fitness(self.x[i]) < self.fitness(self.p_best[i]):
self.p_best[i] = self.x[i]
if self.fitness(self.x[i]) < self.fitness(self.g_best):
self.g_best = self.x[i]
def pso(self):
best = []
self.final_best = np.array([1, 2, 3, 4])
for gen in range(self.time):
self.update(self.size)
if self.fitness(self.g_best) < self.fitness(self.final_best):
self.final_best = self.g_best.copy()
print('当前最佳位置:{}'.format(self.final_best))
temp = self.fitness(self.final_best)
print('当前的最佳适应度:{}'.format(temp))
best.append(temp)
t = [i for i in range(self.time)]
plt.figure()
plt.plot(t, best, color='red', marker='.', ms=15)
plt.rcParams['axes.unicode_minus'] = False
plt.margins(0)
plt.xlabel(u"迭代次数") # X轴标签
plt.ylabel(u"适应度") # Y轴标签
plt.title(u"迭代过程") # 标题
plt.show()
if __name__ == '__main__':
time = 100
size = 100
dimension = 4
v_low = -0.5
v_high = 0.5
low = [-5, -5, -5, -5]
up = [5, 5, 5, 5]
a = [0.1957, 0.1947, 0.1735, 0.16, 0.0844, 0.0627, 0.0456, 0.0342, 0.0323, 0.0235, 0.0246]
b = [0.25, 0.5, 1, 2, 4, 6, 8, 10, 12, 14, 16]
pso = PSO(dimension, time, size, low, up, v_low, v_high, a, b)
pso.pso()
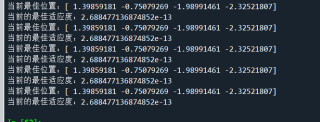
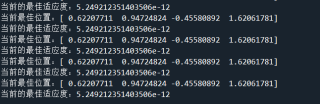
是代码哪里错误了吗,还是粒子群算法结果就是这样的,希望能给出错误地方或者解决这个问题的代码。

