请问如何实现多次仿真结果仿真?
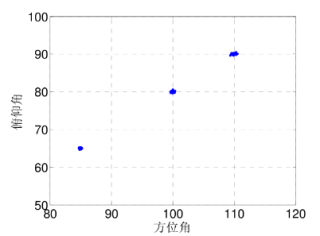
问题描述:以下代码是仿真一次得到的结果,如何得到仿真100次以上的结果,并绘制出类似下面的图片。
其中结果一个为方位角,一个为俯仰角。(图片是仿真几百次后点的汇集点)
clear all
close all
derad=pi/180;
radeg=180/pi;
twpi=2*pi;
kelmx=8;
kelmy=10;
dd=0.5;%阵元间隔
dx=0:dd:(kelmx-1)*dd;%X轴阵元分布
dy=0:dd:(kelmy-1)*dd;%Y轴阵元分布
iwave=3;%目标数
L=iwave;
theta1=[10 30 50];%波达方向
theta2=[15 35 55];%波达方向
snr=20;%信噪比(dB)
n=200;%快拍数
Ax=exp(-i*twpi*dx.'*(sin(theta1*derad).*cos(theta2*derad)));%X轴上阵元对应的方向矩阵
Ay=exp(-i*twpi*dy.'*(sin(theta1*derad).*sin(theta2*derad)));%Y轴上阵元对应的方向矩阵
S=randn(iwave,n);
X0=Ax*S;%接收信号
X=awgn(X0,snr,'measured');%加入高斯白噪声
Y0=Ay*S;
Y=awgn(Y0,snr,'measured');
Rxy=X*Y';%协方差矩阵
P=5;
Q=6;
...............%构造增广矩阵%................
Re=[];
for kk=1:kelmx-P+1
Rx=[];
for k=1:P
Rx=[Rx;R_hankel(k+kk-1,Rxy,kelmy,Q)];
end
Re=[Re,Rx];
end
...............%估计uk和vk%................
[Ue,Se,Ve]=svd(Re);
Uesx=Ue(:,1:L);
Uesx1=Uesx(1:(P-1)*Q,:);
Uesx2=Uesx(Q+1:P*Q,:);
Fx=pinv(Uesx1)*Uesx2;
[EVx,Dx]=eig(Fx);
EVAx=diag(Dx).';
for im=1:Q
Uesy(((im-1)*P+1):P*im,:)=Uesx(im:Q:(im+Q*(P-1)),:);
end
Uesy1=Uesy(1:(Q-1)*P,:);
Uesy2=Uesy(P+1:P*Q,:);
Fy=pinv(Uesy1)*Uesy2;
[EVy,Dy]=eig(Fy);
EVAy=diag(Dy)';
F=0.5*Fx+0.5*Fy;
[EV,D]=eig(F);
P1=EV\EVx;
P2=EV\EVy;
P1=abs(P1);
P2=abs(P2);
P11=P1';
P21=P2';
[c,Px]=max(P11);
[cc,Py]=max(P21);
EVAx=EVAx(:,Px);%估计出uk
EVAy=EVAy(:,Py);%估计出vk
...............%估计出DOA%................
theta10=asin(sqrt((angle(EVAx)/pi).^2+(angle(EVAy)/pi).^2))*radeg;
theta20=atan(angle(EVAy)./angle(EVAx))*radeg;
引用函数
function R=R_hankel(m,Rxy,N,Q)
R1=[];
R2=[];
for mm=1:Q
R1=[R1;Rxy(m,mm)];
end
for i=1:N-Q+1
R2=[R2,Rxy(m,i+Q-1)];
end
R=hankel(R1,R2);
